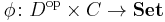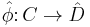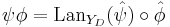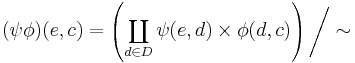Profunctor

In category theory, a branch of mathematics, profunctors are a generalization of relations and also of bimodules. They are related to the notion of correspondences.

1 Definition
- 1.1 Composition of profunctors
- 1.2 The bicategory of profunctors
2 Properties
- 2.1 Lifting functors to profunctors
3 References
4 See also

Definition

A profunctor (also named distributor by the French school and module by the Sydney school) 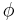$\,\phi$ from a category $C$ to a category $D$ , written

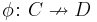$\phi \colon C\nrightarrow D$ ,

is defined to be a functor

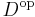$\phi \colon D^{\mathrm{op}}\times C\to\mathbf{Set}$

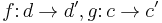where $D^\mathrm{op}$ denotes the opposite category of $D$ and $\mathbf{Set}$ denotes the category of sets. Given morphisms $f\colon d\to d', g\colon c\to c'$ respectively in 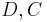$D, C$ and an element 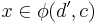$x\in\phi(d',c)$ , we write 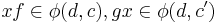$xf\in \phi(d,c), gx\in\phi(d,c')$ to denote the actions.

Using the cartesian closure of 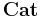$\mathbf{Cat}$ , the category of small categories, the profunctor $\phi$ can be seen as a functor

$\hat{\phi} \colon C\to\hat{D}$

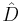where $\hat{D}$ denotes the category 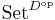$\mathrm{Set}^{D^\mathrm{op}}$ of presheaves over $D$ .

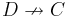A correspondence from $C$ to $D$ is a profunctor $D\nrightarrow C$ .

Composition of profunctors

The composite 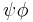$\psi\phi$ of two profunctors

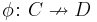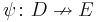
$\phi\colon C\nrightarrow D$ and $\psi\colon D\nrightarrow E$

is given by

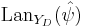$\psi\phi=\mathrm{Lan}_{Y_D}(\hat{\psi})\circ\hat\phi$

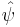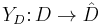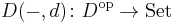where $\mathrm{Lan}_{Y_D}(\hat{\psi})$ is the left Kan extension of the functor $\hat{\psi}$ along the Yoneda functor $Y_D \colon D\to\hat D$ of $D$ (which to every object $d$ of $D$ associates the functor $D(-,d) \colon D^{\mathrm{op}}\to\mathrm{Set}$ ).

It can be shown that

$(\psi\phi)(e,c)=\left(\coprod_{d\in D}\psi(e,d)\times\phi(d,c)\right)\Bigg/\sim$

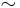where $\sim$ is the least equivalence relation such that 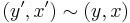$(y',x')\sim(y,x)$ whenever there exists a morphism $v$ in $D$ such that

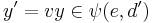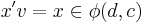$y'=vy \in\psi(e,d')$ and $x'v=x \in\phi(d,c)$ .

The bicategory of profunctors

Composition of profunctors is associative only up to isomorphism (because the product is not strictly associative in Set). The best one can hope is therefore to build a bicategory Prof whose

0-cells are small categories,
1-cells between two small categories are the profunctors between those categories,
2-cells between two profunctors are the natural transformations between those profunctors.

Properties

Lifting functors to profunctors

A functor 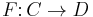$F \colon C\to D$ can be seen as a profunctor 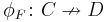$\phi_F \colon C\nrightarrow D$ by postcomposing with the Yoneda functor:

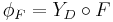$\phi_F=Y_D\circ F$ .

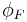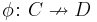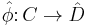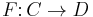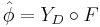It can be shown that such a profunctor $\phi_F$ has a right adjoint. Moreover, this is a characterization: a profunctor $\phi \colon C\nrightarrow D$ has a right adjoint if and only if $\hat\phi \colon C\to\hat D$ factors through the Cauchy completion of $D$ , i.e. there exists a functor $F \colon C\to D$ such that $\hat\phi=Y_D\circ F$ .

References

Bénabou, Jean (2000). Distributors at Work. http://www.mathematik.tu-darmstadt.de/~streicher/FIBR/DiWo.pdf.
Borceux, Francis (1994). Handbook of Categorical Algebra. CUP.

Lurie, Jacob (2009). Higher Topos Theory. Princeton University Press.